Tabeller för resultat av regressionsanalys¶
När man gjort en statistisk analys är det viktigt att presentera resultaten på ett överskådligt och pedagogiskt sätt. Ofta handlar det om en kombination av text, tabeller och grafik. Syftet ska vara att presentera så mycket information att läsaren får med sig de viktigaste slutsatserna och har möjlighet att se hur de dragits, men utan att överlasta med för mycket. Särskilt gäller det siffror som man inte tolkar eller kommenterar i texten.
Statas normaloutput efter regressionsanalys är inte lämplig för publicering. Man kan visserligen själv plocka ut de viktigaste uppgifterna och göra en egen tabell i till exempel Word, men det finns enklare sätt, med tilläggskommandon.
Ett sådant är esttab. I den här guiden kommer vi gå igenom hur man använder det för att göra en enkel och snygg regressionstabell. Men först måste vi installera esttab, eftersom det inte följer med Stata som standard. Det gör vi genom att skriva följande (och det behöver man bara göra en gång):
ssc install estout, replace
Sedan laddar vi in data. I det här exemplet använder vi QoG-institutets QoG Basic data, version 2018. Man kan antingen ladda ned den till sin dator och öppna den där, eller ansluta till den direkt, som jag gör här.
use "https://www.qogdata.pol.gu.se/dataarchive/qog_bas_cs_jan18.dta", clear
Hypotes: Demokrati är bra för livslängd¶
Analysenheten är här länder. Vi ska göra en enkel analys där vi ska undersöka det möjliga sambandet mellan demokrati och förväntad livslängd. Lever folk längre i demokratier? Och i så fall, håller det sambandet under kontroll för andra variabler, till exempel geografisk placering? Vissa teorier säger att demokratier haft lättare att etablera sig i mer tempererade klimat, långt bort från ekvatorn. Och där är det dessutom mindre tropiska sjukdomar.
Om demokrati är bra för hälsan borde vi finna ett samband mellan demokrati och livslängd, och det sambandet borde hålla även under kontroll för landets geografiska placering.
Variablerna vi ska använda är:
Förväntad livslängd: wdi_lifexp
Grad av demokrati: p_polity2 (-10 till -10)
Avstånd från ekvatorn: lp_lat_abst
Nedan visas beskrivande statistik för de tre variablerna.
sum wdi_lifexp p_polity2 lp_lat_abst
Spara resultat av regressionsanalyser med estimates store¶
Vi ska göra tre regressionsanalyser. Först med demokrati som oberoende variabel, sedan med avstånd från ekvatorn, och sedan med både demokrati och avstånd från ekvatorn. Efter varje analys vi gör skriver vi estimates store m1 där m1 är namnet på en modell (som vi hittar på själv). Jag brukar döpa modellerna till m1, m2, m3 och så vidare. I blocket nedan kör jag de tre analyserna och sparar resultaten efter varje analys.
reg wdi_lifexp p_polity2
estimates store m1
reg wdi_lifexp lp_lat_abst
estimates store m2
reg wdi_lifexp p_polity2 lp_lat_abst
estimates store m3
Presentera resultaten med esttab¶
Som synes är resultattabellerna ganska otympliga, och innehåller mycket information som vi vanligtvis inte är intresserade av. Till exempel uttrycker standardfel, t-värde, p-värde och konfidensintervall ungefär samma sak - graden av osäkerhet kring koefficientens skattning. Man behöver inte redovisa alltihopa. Vanligt inom samhällsvetenskap är att man redovisar koefficienten, standardfelet (eller t-värdet) och sätter ut stjärnor som visar signifikansnivån (alltså p-värdet).
esttab gör mycket av detta automatiskt. För att göra en minimal tabell av de tre analyserna vi gjort skriver vi bara:
esttab m1 m2 m3
Mycket bättre! Varje kolumn representerar en analys - en "modell." Längst upp anges vad som var beroende variabel i analysen. Siffrorna visar b-koefficienterna för respektive variabel. Inom parenteserna står t-värdet, och längst ner n-talet.
Vi ser då att i den första modellen finns det ett signifikant samband mellan demokrati och förväntad livslängd - varje steg upp på demokratiskalan hänger ihop med en ökning av livslängden på 0.394 år. Men vi ser också i modell 2 att länder som ligger längre bort från ekvatorn har högre förväntad livslängd. Och vi vet (men det syns inte här) att länder längre bort från ekvatorn har högre grader av demokrati. Så när vi kontrollerar för avstånd från ekvatorn i modell 3 ser vi att koefficienten för demokrati mer än halveras, till 0.155, och den är inte heller längre statistiskt signifikant (vilket vi ser eftersom det inte är några stjärnor utsatta, och t-värdet är under 1.96).
Men det finns också annat vi skulle vilja se i tabellen, till exempel R2-värdet, eller det justerat R2. Och vi kanske hellre vill ha standardfelet inom parenteser, istället för t-värdet. Då kan vi lägga till options på vårt esttab-kommando. Man väljer själv vad man vill lägga till. Använd help esttab för att se en fullständig lista.
esttab m1 m2 m3, se r2 ar2
Den här tabellen är överskådlig och lätt att läsa. Enda problemet är att den inte är så lätt att klistra in i ett Worddokument. Om man gör det måste man sätta typsnittet till courier eller något annat där alla bokstäver är lika stora, annars kommer alla siffror hamna fel.
Men ett bättre sätt är att exportera tabellen till en separat fil som är anpassad för till exempel Word. Då kan man sedan öppna den filen och kopiera tabellen därifrån in i sin rapport.
För att exportera filen lägger vi till using "filnamn.rtf" i koden. Då sparas filen i den aktiva mappen. Den anger man genom att skriva cd "/Users/mindator/statistiskanalys" till exempel. Jag lägger också till replace som option, vilket betyder att om det redan fanns en sådan fil så ska den skrivas över.
esttab m1 m2 m3 using "regressiontabell.rtf", se r2 ar2 replace
Om man sedan öppnar filen med Word ser det ut på följande sätt:
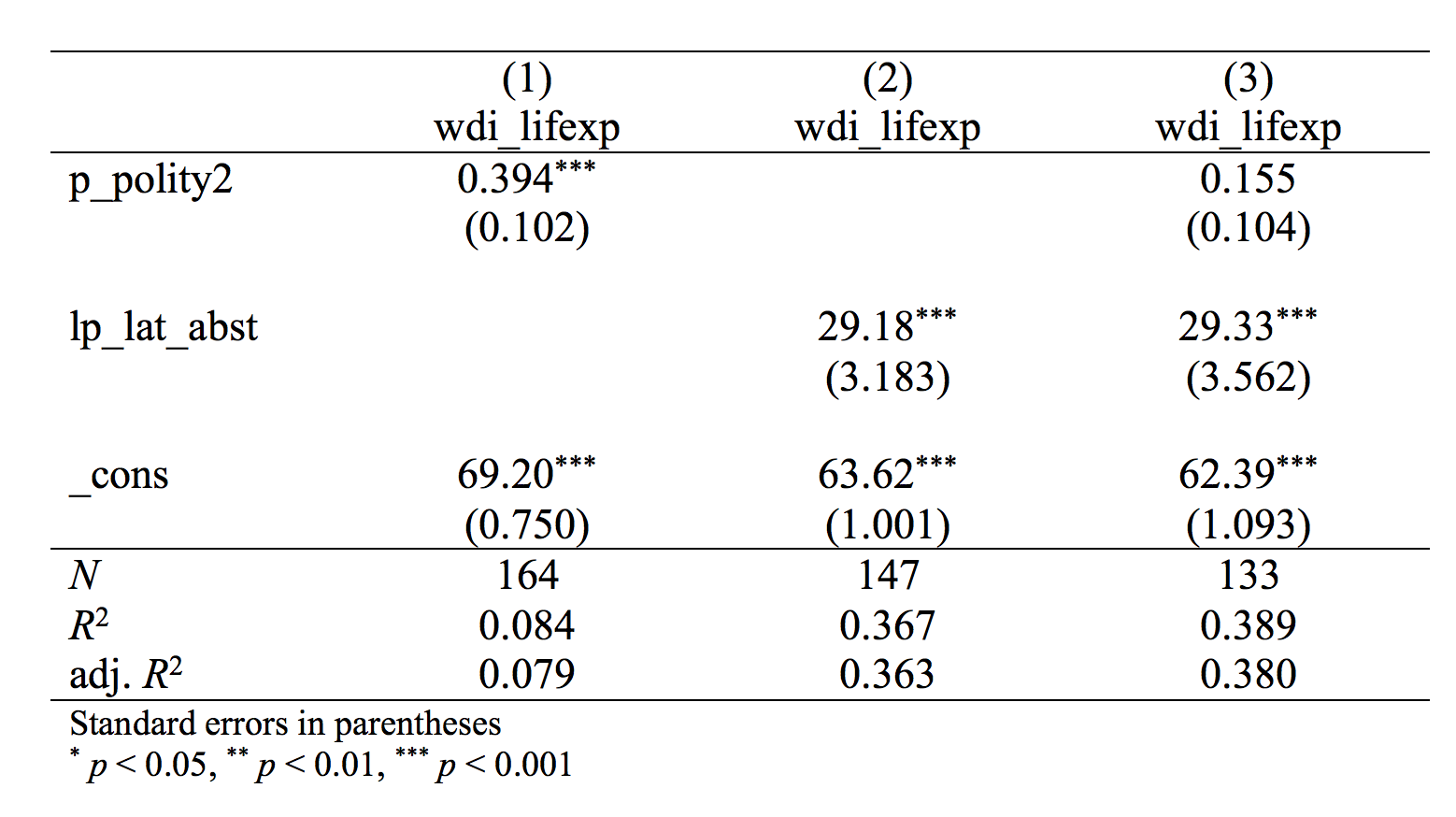
Sedan kan man naturligtvis göra det ännu mer pedagogiskt genom att byta ut variabelnamnen till förklarande etiketter, till exempel "Demokrati (-10 till 10)" eller motsvarande. Men det här är ändå ett stort lyft jämfört med den råa outputen.
Avslutning¶
Att göra tabeller med esttab kräver alltså tre steg. Först gör man analysen, sedan sparar man resultaten från den med estimates store och sedan presenterar man resultaten med esttab.
Tänk på att alltid försöka vara maximalt pedagogisk och tydlig. Den som förlorar mest på att läsaren inte förstår dina resultat är du!